Commentaries on Representation

The Blog for Thirty-Thousand.org

Commentaries on Representation

The Blog for Thirty-Thousand.org

The Cube Root Model: It’s not the law, it’s a suggestion!

The cube root “law” is frequently cited in articles and papers about determining the optimal size of legislative bodies. That’s surprising, because not only is its underlying reasoning profoundly flawed, but the resulting increase in representation would not ameliorate any of the problems it is supposed to address.

When I first heard of the “Cube Root Law”, it was accompanied by a scientific-looking chart with a curved graph like the one below. Like most people, I initially assumed that it was an incontrovertible principle, like Boyle’s Law or the Law of Gravity. You know, a law, something to be obeyed!

Figure 1

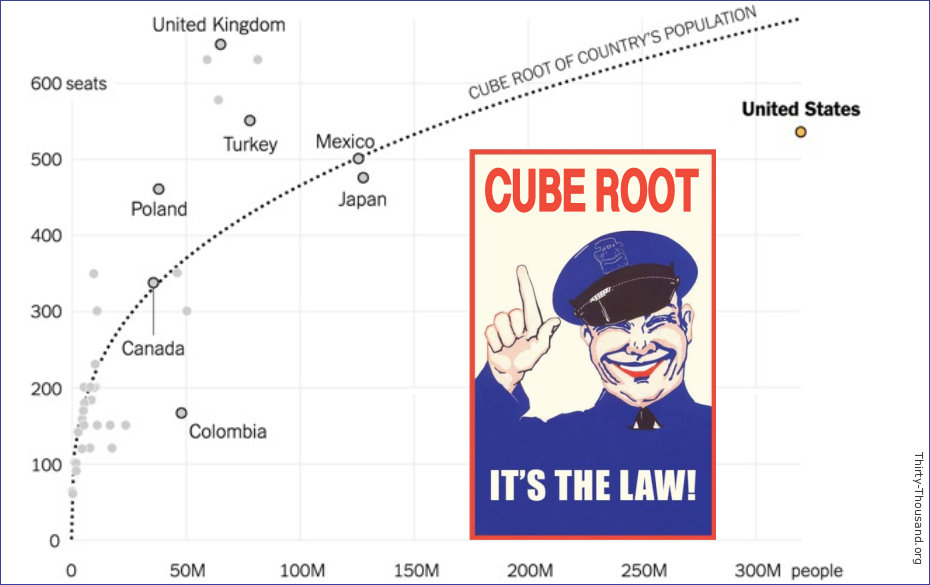
Variously called either a “law” or a “rule”, the cube-root model was proposed by Rein Taagepera in a paper published in 1972.¹ In that paper, he posited that “efficiency is optimized” if the size a national legislature is equal to the third root, or cube root, of that nation’s total population (explained below). In the fifty years since Taagepera’s paper was published, the cube-root model somehow became elevated to a law which has been cited in numerous papers and articles. Presumably a lot of its appeal is its simplicity, but I cannot help but wonder if its inexplicable popularity can be attributed, on some subconscious level, to its focus on an integer that has an exceptionally ancient mystical history.² I don’t believe that the “2.22-root law” would have been quite as catchy, for example.

The Problem: The U.S. House of Representatives is far too small

Because our House of Representatives has been arbitrarily fixed at 435 members for well over a century, there is a growing awareness that having a House which is “far too small … poses a big danger to American democracy”.³ The U.S. House is indeed far too small to properly represent the American people, and the numerous problems resulting therefrom are explained elsewhere in this website.

So though there is a growing consensus that our House is far too small, determining the size it should be seems to be a difficult question to answer. However, as mentioned in the conclusion to this commentary, there is a widely-accepted mathematical criteria that leads to a logical and irrefutable solution. Since that solution is generally overlooked, or disregarded, scholars and others grasp for a defensible rationale for enlarging the House other than simply choosing a larger arbitrary number to replace the current arbitrary number.

The Cube-Root Model

The so-called Cube-Root Law, which is the subject of this commentary, appears to be the most widely cited algorithm for determining the size of the House.⁴ Before getting into the cube-root model itself, the first thing which should be pointed out is that increasing the size of the U.S. House to that indicated by the cube root model would result in far too few Representatives to have any material impact on the problems it is supposed to eliminate. So, even if the reasoning underlying this concept were faultless, it would be, in reality, a solution that does not solve.

Beyond its ineffectiveness, when I finally got around to digging into the cube-root proposition itself, I was surprised to realize how fundamentally flimsy it is for two reasons. First, as explained below, it is derived from a mathematical average of a broad range of nations. While that may be a plausible way to establish a benchmark, it certainly does not establish an ideal standard given the heterogeneous mix of nations relative to their forms of government and the quality thereof.

And second, though it is said that the sizes of most of the national legislatures map closely to its cube root prediction, that depends on what is meant by “close” – science close or atomic bomb close?

I long wondered if I were the only one who noticed these deficiencies with the cube-root model but thankfully, as noted later in this commentary, there is now credible scholarly support for these criticisms. However, before getting into the flawed reasoning upon which the cube-root model was derived, a Cube Roots for Dummies primer in in order.

A brief primer on the cube-root formula

If you’re math-phobic, don’t worry: This is as easy as 2 × 2 × 2 = 8. In that example, 2 is the third root of 8, which is also called the “cube root”. That’s it! All of the equations below are just different ways of expressing the exact same formula:

2 × 2 × 2 = 8.
2³ = 8.
∛8 = 2 (the 3 on top of the √ is called the index).
8^⅓ = 2 (the ⅓ is called the exponent).

The chart below is merely a graph of the cube-root formula itself, wherein the horizontal “x-axis” is in millions, and its corresponding cube root is indicated on the vertical “y-axis”.

Figure 2

As an example: The cube root of 125 million (x-axis) is 500 (y-axis). Listed on the chart are the various ways that can be expressed mathematically.

For every point on the curve, the X value is equal to Y × Y × Y, or Y³. Alternatively, the Y value is equal to the third root of X (or ∛X).

Next: Add some data points to the chart

For this analysis, rather than using the 120-nation dataset that was the basis of Taagepera’s 1972 paper, I will rely on the dataset used in a 2020 report issued by the Fordham University School of Law⁵ (which used 2015 population and legislature data as the basis of their analysis). The Fordham report limited their data set to the 37 OECD member nations,⁶ all of which have democratically elected national legislatures. For each of those OECD nations, the chart above will be used to illustrate the relationship between the size of its national legislature and its total population.

Let’s begin by only plotting the U.S. onto the chart (below), which had a total population of approximately 320 million (x-axis), and 535 members of Congress (y-axis). Note that, for their analysis, Fordham added the total number of Senators (100) to 435 Representatives to arrive at 535. And even based on that larger size, U.S. legislature is still well below the benchmark of 684 suggested by the cube root model. Of course, we already knew that our House of Representatives was far too small, but thanks for confirming.

Figure 3

The chart below adds the remaining OECD member nations (listed in the text box inset into the chart), plotted in the same manner as the U.S. on the preceding chart.

Figure 4

In the chart above, a few of the nations are identified in order to provide some reference points. (The number in parentheses next to each country is its “index” – explained later.) For example, the United Kingdom’s 650-member House of Commons is much larger than the size suggested by the cube root model (403). And at 166 members, Columbia’s Chamber of Representatives is well below the cube root of its population (364). The supporting data for all these nations are provided here.

So all we have at this point is a chart with graph representing a mathematical equation (∛), which is also decorated with the plots of 37 nations. In other words, all we have so far is art, and no science. So how did the cube-root formula become the law? Well, that requires some imagination. 🌈

Divining a cube-root pattern

In the chart above, note that the national legislature sizes of many of the countries appear to be close to the third root (∛) graph, but appearances can be deceiving. Before explaining why, here’s a little handy math lingo: The “3” in the ∛ is known as the “index”. (By the way, the little “√” thing is called the “radical sign”, and the number inside of it is the “radicand” – don’t worry, that’s not going to be on the test.) For example, in the equation below, “n” is the index.

If a country’s index (n) were exactly 3.0, then it would be plotted right on top of the ∛ graph (and a few are very close). However, if its index is not 3, then what is it? It’s going to be a non-integer (or decimal) number such as 3.12. Don’t try to understand non-integer indexes (unless you really want to⁷) as that’s a job for a calculator!

Returning to the last chart (Figure 4), the rounded index values are indicated for those nations identified therein. For example, the U.S. index (n) is equal to 3.12 (or 3.1172840006 to be more exact). That means that the size of the US legislature (535) is the 3.12 root of the total population, as follows:

Of course, that’s the same as (National Legislature Size)^3.12 = Population.

At it turns out, not one single country had a legislature size which was exactly equal to the cube root of its total population; that is, with an index (n) equal to 3.0. However, here are the three nations that came closest, listed in order:

Mexico: n = 3.001143
Denmark: n = 2.998436
Switzerland: n =3.001143

For this data set, the index values range from 2.75 (Sweden) to 3.49 (Chile) – both of which are identified on the chart above.

Note that those legislatures which are smaller than the cube-root benchmark (below the graph) have an index > 3.0. And the legislatures larger than the benchmark (above the graph) have an index < 3.0. A simple math example shows why the size of the legislature gets bigger as the index gets smaller: The square root of 64 is 8 (√64 = 8). Now increase the index from 2 to 3: The cube root of 64 is 4 (∛64 = 4).

So, given this range of values, how did the cube root become law?

As it turns out, the arithmetic average of all 37 indexes is 3.06 (those index values are provided here). This pattern, of the average of the indexes being approximately 3.0, was first observed in Taagepera’s 1972 paper mentioned earlier. It was that observation that gave rise to the notion that the optimal size of any nation’s legislature is the cube root of its total population.

The reality: Orders of magnitude

Looking back at Figure 4, the fact that many of the nations’ index values appear to be so close to the cube-root graph is very misleading, especially for those who are unaccustomed to the mathematics of exponents. To illustrate the power of exponents, consider the Richter Scale which is commonly referenced when describing the magnitude of earthquakes: A 4.2 earthquake may not seem like it would be much more powerful than one measuring 4.0, but its magnitude is actually 58% more intense! Why? Because (10^4.2) is 58% larger than (10⁴). Such is the nature of the mathematics of exponents.

Similarly, small differences in index values result in deviations in the legislature sizes of significant magnitude. For each OECD nation, the bar chart below indicates the percentage difference between the actual size of its legislature and its cube-root benchmark, scaled against the left-hand y-axis.

Figure 5

Also indicated in the chart above, by the small diamond (◆), is the index (n) value for each OECD nation scaled against the right-hand y-axis.

The chart illustrates that seemingly tiny differences between n and the cube root actually indicate that the sizes of these countries’ legislatures are significantly different than their cube-root benchmarks. For example, the U.S. index (3.117284) would seem to be fairly close to 3. And yet the U.S. Congress is 22% smaller than its cube-root benchmark. Another example: The German index is 2.83, which seems pretty close to its cube root, but the Bundestag would have to reduce its membership by 45% to conform to the cube-root benchmark! (As noted above, as the index gets smaller, the legislature gets larger relative to its cube-root benchmark.)

A specious conclusion

These seemingly tiny differences in index values are deceptive: Based on the data set presented above, one report stated that the “size of most of the legislatures is either very close to the cube root of the population or contains more representatives than the cube root would suggest”.⁸ Yes, perhaps “very close” with respect to their index (n) values but, for all 37 nations, the average difference between their actual legislature sizes and their cube-root benchmarks is over 24%! And over half of the countries’ legislature sizes vary from the cube-root by over 20%. That ain’t “very close”.

Therefore, when you consider how much the legislature sizes vary from their cube-root benchmarks, it requires a big stretch of the imagination to divine a cube-root law from a simple average of these widely dispersed index values.

Putting aside the illusion that the sizes of many of the legislatures are “very close” to the cube root, the next problem is with respect to the underlying concept: It is absurd to assert that the average of any group represents some kind of ideal. That would be like saying that your ideal body weight should be the average weight of a cross-sample of adults visiting Disney World. And moreover, imagine if that sample disregarded whether some adults were taller than others, or how healthy their lifestyles are, the mixture of men and women, or whether any of the women were pregnant. And what if this same group were measured again years later and the average changed, does that mean the ideal has changed?

Consider the disparate forms of government that comprise the OECD, especially in comparison with the U.S. Only five of them are multi-state federal republics,⁹ the remainder being various implementations of parliamentary systems. And of those federal republics, the U.S. has the largest number of states by far (as well as the largest population and greatest land mass).

And regarding the effect of the dataset changing over time, in 2019 Italy voted to reduce the size of its Chamber of Deputies from 630 to 400.¹⁰ If this and other such changes were to alter the average index from 3, should the “ideal” legislature size therefore be changed?

The foregoing is my own take on the cube-root model’s considerable shortcomings. Fortunately, you don’t have to take my word for it: A far more scholarly examination of the cube-root “law” has thoroughly debunked it.

The Cube-Root Law is Conceptually Flawed

In a paper published in 2021, a distinguished physicist and emeritus professor at École Polytechnique Fédérale de Lausanne, Giorgio Margaritondo,¹¹ evaluated Taagepera’s original paper which was the basis for the cube-root “law”. His conclusions are revealed in the title of his paper: The Classic Derivation of the Cube-Root Law is Conceptually Flawed.¹²

Dr. Margaritondo’s evaluation is far more scholarly and rigorous than my commentary above. It is recommended reading for anyone seeking a deeper understanding of the critical problems with the cube-root model which, as explained in his paper, are as follows:

The cube-root law was not derived from its data and the corresponding fit was arbitrarily forced.
The theoretical steps that were used to derive the cube-root formula incorrectly evaluated one of its key factors.
The model assumed that each representative spends on the average equal times for communications inside and outside the parliament, an arbitrary hypothesis that has unrealistic consequences.
No evaluation of the “optimal” size based on a power law, including the cube-root one, can reach a meaningful accuracy.

Relative to Taagepera’s paper, the first point is the most damning: The cube-root formula was force-fitted onto the dataset. That helps to explain the significant disparities between the actual legislature sizes and their cube-root benchmarks (as illustrated in Figure 5). But the bigger reason for those disparities is that no such equation can do the job, which is his fourth point. It is this last point which is the most significant relative to this subject. As stated in his paper, “the assembly size evaluation exceeds the accuracy of all power equations, which cannot be reliably used for political analysis”. Margaritondo substantiates this point with a least-squares regression analysis, demonstrating that there is no single equation which precisely fits the data.

Elaborating on that point further, Margaritondo observed that:

Politicians should respect science much more, but we’re not helping by proposing science for issues for which it’s not made. To think that we can accurately derive the optimal parliament size with a power law is an illusion.¹³

It absolutely is an illusion to imagine there is a universal one-size-fits-all equation which could define the optimal size of any nation’s legislature. This is especially true relative to Taagepera’s 120-nation dataset given the strikingly disparate forms of government included therein. And, like the Fordham analysis discussed above, that list includes very few multi-state federal republics comparable to the U.S.

Making matters worse, Taagepera’s list included such charming travel destinations as Afghanistan, Central African Republic, Libya, Pakistan, etc. As Margaritondo observed, Taagepera’s analysis “tried to link the populations not to the ‘optimal’ parliament sizes but to the real sizes, using data for countries of all kinds. Of these, many if not most were plagued by corruption, ineffective bureaucracy and/or authoritarian regimes. Thus, they could hardly lead to ‘optimal’ values of [legislature sizes].” (This is the point I made, less eloquently, with my analogy to choosing your ideal body weight based on the average weight of adults visiting Disney World.)

Dr. Margaritondo’s paper concludes with the following summary:

In short, accurately evaluating the “optimal” size of a national assembly is illusory. And trying to inject additional factors besides the population cannot solve the above problems.

At most, this kind of approach can identify the countries that strongly deviate from the “average”, [such as] France, the USA and Italy. However, without filtering the “average” is for a mix of “good” and “bad” countries, thus a deviation from it is not necessarily negative . . .and could even be positive!

In conclusion, we surprisingly found that the historical and very influential work of Taagepera used a wrong equation to derive its famous cube-root law and arbitrarily assumed time equipartition between inter-assembly and assembly-constituency communications. An unrestricted best fit of the original data does not support the cube-root law and would favor instead a power law with an exponent larger than ⅓. These flaws fatally undermine the foundations of the cube-root law and disqualify – also for other reasons – its popular use to evaluate the “optimal” parliament size for a country.

In Taagepera’s defense, however, he did concede that his approach involves “all sorts of simplifying assumptions”, adding that it should be accepted “cautiously, as a possible guideline until something better comes about.”¹⁴ It is probably not his fault that various “experts” disregarded his caution, grabbed his cube-root football, then ran out of the stadium and down the street.

The Cube-Root Preemption

If the size of U.S. House were increased to that indicated by the cube-root model, it would have virtually no effect on the various problems it is ostensibly supposed to alleviate. Based on the 2020 census, the cube-root House would have 692 Representatives,¹⁵ resulting in an average district (or constituency) size of 478,480.¹⁶ Though that would be smaller than the current average size, the congressional districts would still be so massive that the candidates’ dependence on Special Interests funding would continue unabated. In fact, the U.S. congressional districts would still be the largest in the world, and almost twice as large as second-place Mexico.¹⁷

In addition, the size of these districts would still be grossly unequal from state to state. In fact, with 692 Representatives, the largest congressional district would be 75% more populous than the smallest, a negligible improvement over the current disparity of 82% (relative to 435 districts). These inequitable disparities would therefore extend to the states’ representation in the Electoral College.

And though having 692 Representatives (instead of 435) would likely increase the diversity of our representation to some extent, there is no reason to believe that its impact would be more than marginal.

To summarize, even if the the cube-root model were not conceptually flawed, it is a solution that does not actually solve any problems. From the perspective of the average citizen, there is no reason to believe that increasing the the number of Representatives from 435 to 692 would improve his or her life in any meaningful way—the citizenry would continue to be just as powerless as we are now under the Regime of 435.

Finally, making the cube-root formula into law would actually provide an ostensible rationale for keeping our representation small enough to protect the political status quo, thereby securing the continued reign of America’s ruling class. That is, a cube-root “law” would be, in effect, a preemptive measure to prevent the House from ever growing to the size necessary to achieve a truly representative government.

The Founders’ Rule

The good news is that there is a mathematical formulation for determining how many Representatives we should have in the U.S. House: The Founders’ Rule would ensure compliance with the language of the Constitution as well as the Fourteenth Amendment. Not only would it eliminate all the problems that the cube-root model does not, but this is the solution that was intended to be mandated by the first amendment proposed for the Bill of Rights. Because this solution is congruous with the Constitution’s one-person-one-vote requirement, it should be quite obvious; however, it is generally ignored. Why? Because it would restore true representative government; that is, it would restore the Peoples’ House.